12 KiB
This document provides an overview of how Klipper implements robot motion (its kinematics). The contents may be of interest to both developers interested in working on the Klipper software as well as users interested in better understanding the mechanics of their machines.
Acceleration
Klipper implements a constant acceleration scheme whenever the print head changes velocity - the velocity is gradually changed to the new speed instead of suddenly jerking to it. Klipper always enforces acceleration between the tool head and the print. The filament leaving the extruder can be quite fragile - rapid jerks and/or extruder flow changes lead to poor quality and poor bed adhesion. Even when not extruding, if the print head is at the same level as the print then rapid jerking of the head can cause disruption of recently deposited filament. Limiting speed changes of the print head (relative to the print) reduces risks of disrupting the print.
It is also important to limit acceleration so that the stepper motors do not skip or put excessive stress on the machine. Klipper limits the torque on each stepper by virtue of limiting the acceleration of the print head. Enforcing acceleration at the print head naturally also limits the torque of the steppers that move the print head (the inverse is not always true).
Klipper implements constant acceleration. The key formula for constant acceleration is:
velocity(time) = start_velocity + accel*time
Trapezoid generator
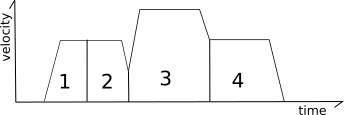
Klipper uses a traditional "trapezoid generator" to model the motion of each move - each move has a start speed, it accelerates to a cruising speed at constant acceleration, it cruises at a constant speed, and then decelerates to the end speed using constant acceleration.
It's called a "trapezoid generator" because a velocity diagram of the move looks like a trapezoid.
The cruising speed is always greater than or equal to both the start speed and the end speed. The acceleration phase may be of zero duration (if the start speed is equal to the cruising speed), the cruising phase may be of zero duration (if the move immediately starts decelerating after acceleration), and/or the deceleration phase may be of zero duration (if the end speed is equal to the cruising speed).
Look-ahead
The "look-ahead" system is used to determine cornering speeds between moves.
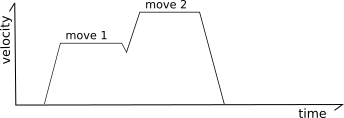
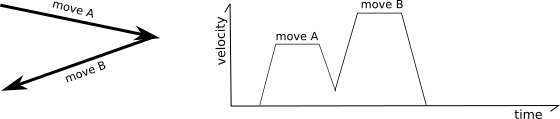
Consider the following two moves contained on an XY plane:
In the above situation it is possible to fully decelerate after the first move and then fully accelerate at the start of the next move, but that is not ideal as all that acceleration and deceleration would greatly increase the print time and the frequent changes in extruder flow would result in poor print quality.
To solve this, the "look-ahead" mechanism queues multiple incoming moves and analyzes the angles between moves to determine a reasonable speed that can be obtained during the "junction" between two moves. If the next move is nearly in the same direction then the head need only slow down a little (if at all).
However, if the next move forms an acute angle (the head is going to travel in nearly a reverse direction on the next move) then only a small junction speed is permitted.
The junction speeds are determined using "approximated centripetal acceleration". Best described by the author.
Klipper implements look-ahead between moves contained in the XY plane that have similar extruder flow rates. Other moves are relatively rare and implementing look-ahead between them is unnecessary.
Key formula for look-ahead:
end_velocity^2 = start_velocity^2 + 2*accel*move_distance
Smoothed look-ahead
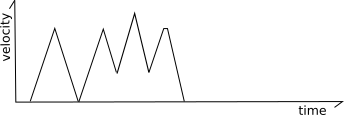
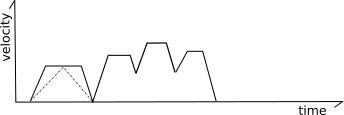
Klipper also implements a mechanism for smoothing out the motions of short "zigzag" moves. Consider the following moves:
In the above, the frequent changes from acceleration to deceleration can cause the machine to vibrate which causes stress on the machine and increases the noise. To reduce this, Klipper tracks both regular move acceleration as well as a virtual "acceleration to deceleration" rate. Using this system, the top speed of these short "zigzag" moves are limited to smooth out the printer motion:
Specifically, the code calculates what the velocity of each move would be if it were limited to this virtual "acceleration to deceleration" rate (half the normal acceleration rate by default). In the above picture the dashed gray lines represent this virtual acceleration rate for the first move. If a move can not reach its full cruising speed using this virtual acceleration rate then its top speed is reduced to the maximum speed it could obtain at this virtual acceleration rate. For most moves the limit will be at or above the move's existing limits and no change in behavior is induced. For short zigzag moves, however, this limit reduces the top speed. Note that it does not change the actual acceleration within the move - the move continues to use the normal acceleration scheme up to its adjusted top-speed.
Generating steps
Once the look-ahead process completes, the print head movement for the given move is fully known (time, start position, end position, velocity at each point) and it is possible to generate the step times for the move. This process is done within "kinematic classes" in the Klipper code. Outside of these kinematic classes, everything is tracked in millimeters, seconds, and in cartesian coordinate space. It's the task of the kinematic classes to convert from this generic coordinate system to the hardware specifics of the particular printer.
In general, the code determines each step time by first calculating where along the line of movement the head would be if a step is taken. It then calculates what time the head should be at that position. Determining the time along the line of movement can be done using the formulas for constant acceleration and constant velocity:
time = sqrt(2*distance/accel + (start_velocity/accel)^2) - start_velocity/accel
time = distance/cruise_velocity
Cartesian Robots
Generating steps for cartesian printers is the simplest case. The movement on each axis is directly related to the movement in cartesian space.
Delta Robots
To generate step times on Delta printers it is necessary to correlate the movement in cartesian space with the movement on each stepper tower.
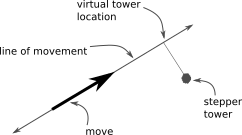
To simplify the math, for each stepper tower, the code calculates the location of a "virtual tower" that is along the line of movement. This virtual tower is chosen at the point where the line of movement (extended infinitely in both directions) would be closest to the actual tower.
It is then possible to calculate where the head will be along the line of movement after each step is taken on the virtual tower.
The key formula is Pythagoras's theorem:
distance_to_tower^2 = arm_length^2 - tower_height^2
One complexity is that if the print head passes the virtual tower location then the stepper direction must be reversed. In this case forward steps will be taken at the start of the move and reverse steps will be taken at the end of the move.
Delta movements beyond simple XY plane
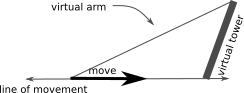
Movement calculation is more complicated if a single move contains both XY movement and Z movement. These moves are rare, but they must still be handled correctly. A virtual tower along the line of movement is still calculated, but in this case the tower is not at a 90 degree angle relative to the line of movement:
The code continues to calculate step times using the same general scheme as delta moves within an XY plane, but the slope of the tower must also be used in the calculations.
Should the move contain only Z movement (ie, no XY movement at all) then the same math is used - just in this case the tower is parallel to the line of movement.
Stepper motor acceleration limits
With delta kinematics it is possible for a move that is accelerating in cartesian space to require an acceleration on a particular stepper motor greater than the move's acceleration. This can occur when a stepper arm is more horizontal than vertical and the line of movement passes near that stepper's tower. Although these moves could require a stepper motor acceleration greater than the printer's maximum configured move acceleration, the effective mass moved by that stepper would be smaller. Thus the higher stepper acceleration does not result in significantly higher stepper torque and it is therefore considered harmless.
However, to avoid extreme cases, Klipper enforces a maximum ceiling on stepper acceleration of three times the printer's configured maximum move acceleration. (Similarly, the maximum velocity of the stepper is limited to three times the maximum move velocity.) In order to enforce this limit, moves at the extreme edge of the build envelope (where a stepper arm may be nearly horizontal) will have a lower maximum acceleration and velocity.
Extruder kinematics
Klipper implements extruder motion in its own kinematic class. Since the timing and speed of each print head movement is fully known for each move, it's possible to calculate the step times for the extruder independently from the step time calculations of the print head movement.
Basic extruder movement is simple to calculate. The step time generation uses the same constant acceleration and constant velocity formulas that cartesian robots use.
Pressure advance
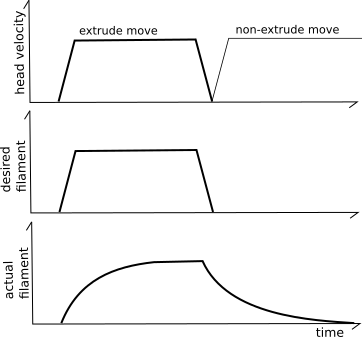
Experimentation has shown that it's possible to improve the modeling of the extruder beyond the basic extruder formula. In the ideal case, as an extrusion move progresses, the same volume of filament should be deposited at each point along the move and there should be no volume extruded after the move. Unfortunately, it's common to find that the basic extrusion formulas cause too little filament to exit the extruder at the start of extrusion moves and for excess filament to extrude after extrusion ends. This is often referred to as "ooze".
The "pressure advance" system attempts to account for this by using a different model for the extruder. Instead of naively believing that each mm^3 of filament fed into the extruder will result in that amount of mm^3 immediately exiting the extruder, it uses a model based on pressure. Pressure increases when filament is pushed into the extruder (as in Hooke's law) and the pressure necessary to extrude is dominated by the flow rate through the nozzle orifice (as in Poiseuille's law). The key idea is that the relationship between filament, pressure, and flow rate can be modeled using a linear coefficient:
extra_filament = pressure_advance_coefficient * extruder_velocity
See the pressure advance document for information on how to find this pressure advance coefficient.
Once configured, Klipper will push in an additional amount of filament during acceleration. The higher the desired filament flow rate, the more filament must be pushed in during acceleration to account for pressure. During head deceleration the extra filament is retracted (the extruder will have a negative velocity).
One may notice that the pressure advance algorithm can cause the extruder motor to make sudden velocity changes. This is tolerated based on the idea that the majority of the inertia in the system is in changing the extruder pressure. As long as the extruder pressure does not change rapidly the sudden changes in extruder motor velocity are tolerated.
One area where sudden velocity changes become problematic is during small changes in head speed due to cornering.
To prevent this, the Klipper pressure advance code utilizes the move look-ahead queue to detect intermittent speed changes. During a deceleration event the code finds the maximum upcoming head speed within a configurable time window. The pressure is then only adjusted to this found maximum. This can greatly reduce (or even completely eliminate) pressure changes during cornering.